Heng Yang
Back to projects
•
3 min read
Probabilistic Pathfinding

This project was designed to teach pathfinding techniques to FIRST Robotics Competition team #9114.

It’s a motion-planning pipeline for a square robot that can translate and rotate on a 2D map. The pipeline:

  1. converts a binary obstacle map into a 3D configuration space (x, y, θ),
  2. computes a Euclidean Distance Field over that space,
  3. constructs a probabilistic roadmap with collision-free edges,
  4. finally runs A* on the roadmap to find a path.

The pipeline persists intermediate artifacts so subsequent runs are faster.

Inputs & outputs

  • Input

    • FIELD.png: grayscale occupancy map (dark = obstacle). Threshold <128 is treated as blocked.
    • Robot model: a square of side s = 80 px with full 360° orientation.

  • Outputs (cached/visual)

    • field.npy, edf.npy: 3D C-space occupancy and Euclidean Distance Field.
    • nodes.pkl, n_adj.pkl: PRM nodes and adjacency.
    • path.png: map with the planned trajectory drawn as oriented squares.

The algorithm

Given an occupancy map of a field like the one below,

  • obstacles are expanded by the footprint of the robot; any pose where the robot would collide with an obstacle is marked blocked.
  • scipy.ndimage.distance_transform_edt is computed on the free configuration space, indicating the clearance to the nearest obstacle at every point.

Files: configurations.py

  • ConfigHelper.make_config_space(...) does the per-angle expansion.
  • ConfigHelper.make_edf() builds the EDF.
  • ConfigSpace stores 3D occupancy, EDF, and provides utilities (distance, edge checking, save/load).

field

Then, it’s onto creating the probabilistic roadmap.

  • Network.add_random_nodes() draws poses using a clearance-dependent PDF, i.e. points closer to obstacles are more likely to be added to the PRM.
  • scipy.spatial.cKDTree is used to calculate nearest neighbors. I had to patch it to allow the angle dimension to wrap at 360°.
  • Sampled nodes are connected via connect_node() to the k nearest neighbors to them. Edges are validated by tracing a 3D Bresenham-like line over (row, col, angle) and rejecting the edge if voxels are blocked.

File: network.py

  • Network.build_tree() builds the k-d tree (periodic in θ).
  • Network.connect_all(k) and connect_node(...) add edges that pass collision checks via ConfigSpace.is_blocked_edge(...).

path

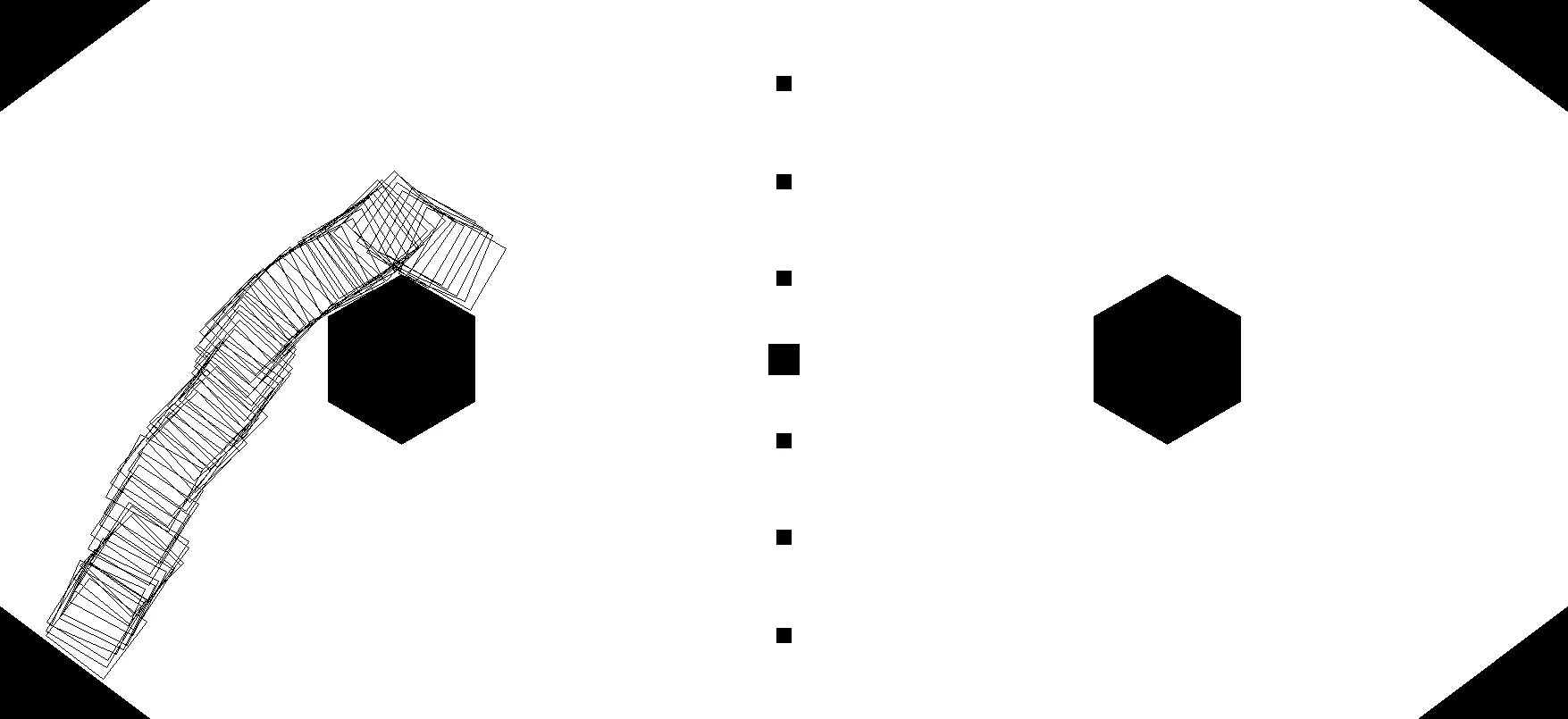
Once the graph is created, A* optimally traverses it from a start pose [e.g. (512, 512, 60°)] to a goal pose [e.g. (108, 101, 53°)]

File: pathfinding.py

  • a_star(...) implements A*,
  • ConfigSpace.distance(...) provides the angle-aware metric.

Running It

# Dependencies
pip install numpy scipy pillow

# Check that the field is in this directory
python main.py

On the first run, it will generate and cache:

  • C-space & EDF: field.npy, edf.npy
  • PRM nodes & edges: nodes.pkl, n_adj.pkl

Subsequent runs reuse these files to go straight to pathfinding.